Revisiting Inverse Steering: Early Behaviour Arbitration and Its Connection to Model Predictive Control

Back in 2003, we introduced a method for real-time action selection in dynamic environments, based on what we called inverse steering behaviours. The idea was to evaluate several possible movement directions at each time step and assign a cost to each, based on how well it satisfied goals like seeking a target, avoiding obstacles, or staying within bounds. These costs were then combined using a hand-crafted heuristic, and the lowest-cost direction was selected.

This model was reactive and modular. Unlike classic steering behaviours that output a direction directly and blend results (typically by weighted averaging), we inverted the process. Each behaviour provided a cost function over candidate actions, and arbitration occurred at the level of outcomes, not actions.

We deployed this model in the context of RoboCup Soccer Simulation, where agents needed to make fast decisions under uncertainty. While the approach was effective in its domain, it was inherently limited by its reliance on hand-designed cost terms and fixed weightings. It had no capacity for learning, long-term reasoning, or generalisation.

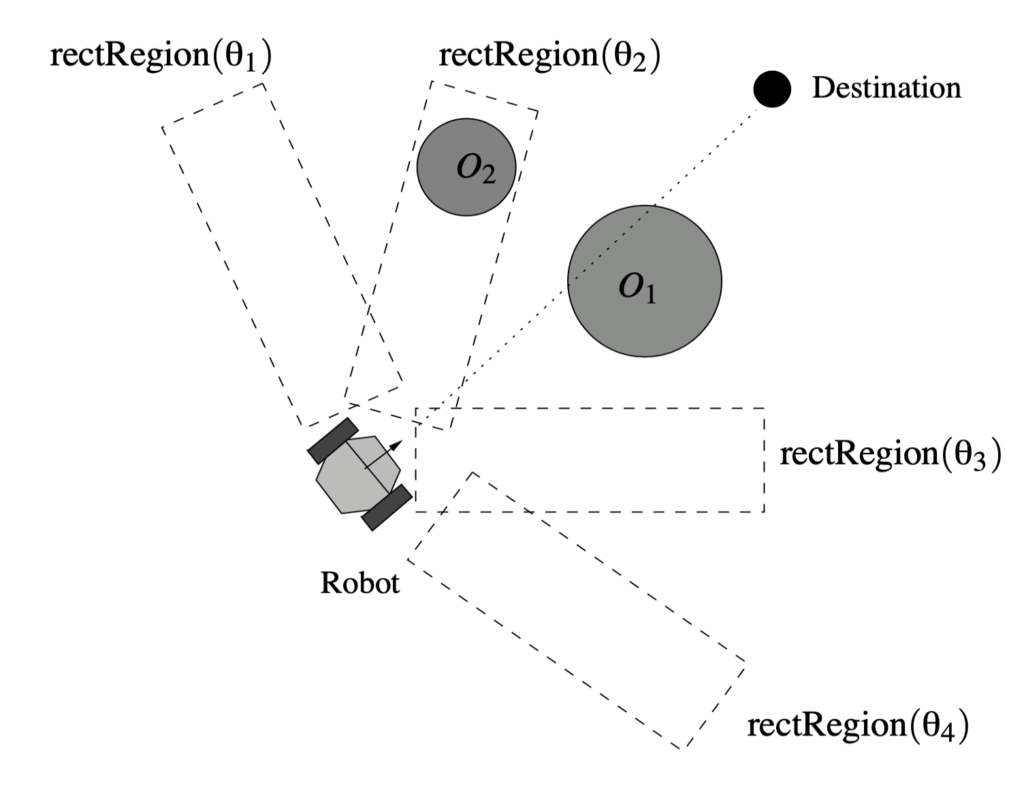
Robot selecting and blending behaviours based on goals

Steering arbitration and one-step planning

Today, we would see this approach as a simplified, hand-crafted version of Model Predictive Control (MPC). In its standard form, MPC selects a control sequence by simulating future states under a dynamics model. This is an optimisation problem that can be written as:

$\begin{aligned} \text{minimise} \quad & \sum_{t=0}^{T - 1} c(x_t, u_t) \\ \text{subject to} \quad & x_{t+1} = f(x_t, u_t), \quad x_0 = x_{\text{current}} \end{aligned}$

In our case, there was no model $f$ , no long-term horizon, and no continuous control sequence. Instead, we performed a one-step lookahead by discretising the action space and evaluating each candidate direction. If $\theta_i$ is the $i$ -th candidate direction and $c_j$ is the cost function from the $j$ -th behaviour, we compute:

$\theta^* = \arg\min_{\theta_i} \; h\left( c_1(\theta_i), c_2(\theta_i), \dots, c_m(\theta_i) \right)$

where $h(\cdot)$ is a heuristic function that combines individual costs. For example, in our RoboCup agent, we used:

$h(\theta) = c_{\text{avoid}}(\theta) + \frac{1}{4} \, c_{\text{contain}}(\theta) + \frac{1}{180} \, c_{\text{seek}}(\theta)$

Strengths and limitations

This type of arbitration captures some of the advantages of MPC, particularly the explicit evaluation of action alternatives. It also retains interpretability and modularity, which are often lost in end-to-end learning systems.

However, there are important limitations:

No prediction of long-term effects beyond the immediate step
Fixed weights and behaviours, requiring manual tuning for new domains
No adaptation or learning from data
No mechanism for handling uncertainty or exploration

By contrast, modern MPC methods typically learn dynamics models or value functions, optimise over longer horizons, and use continuous optimisation or sampling. Hybrid systems may integrate MPC with reinforcement learning, or use model-free policy gradients to learn the cost structure directly.

A modern view

If revisited today, inverse steering could form the backbone of a hybrid control system. The structure of candidate action evaluation remains relevant, but the internals could be learned:

Each behaviour’s cost function 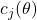$c_j(\theta)$ could be learned from data
The weightings in the aggregator 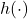$h(\cdot)$ could be optimised based on reward
A learned model could replace geometric collision checks or goal alignment

Such a system would resemble one-step MPC with structured priors, or a policy over discretised actions shaped by behavioural costs. This might be especially relevant in domains where interpretability, robustness, and reaction speed matter more than asymptotic optimality.

Even though today we’d prefer behaviours learned from data and experience, the architectural choices we made for inverse steering behaviours, like evaluating alternatives rather than simply blending outputs, or embedding task knowledge in the scoring function, are still instructive.

References

Ben Amor, H., Obst, O., & Murray, J. (2006). Fast, Neat, and Under Control: Arbitrating Between Steering Behaviors. In AI Game Programming Wisdom 3, pp. 221–232 [preprint rr-12-2003 ].
Thunderhead Engineering. (2024). Pathfinder Technical Reference Manual [Link].